SICP Exercise 3.16
Question
Ben Bitdiddle decides to write a procedure to count the number of pairs in any list structure. “It’s easy,” he reasons. “The number of pairs in any structure is the number in the car plus the number in the cdr plus one more to count the current pair.” So Ben writes the following procedure:
(define (count-pairs x)
(if (not (pair? x))
0
(+ (count-pairs (car x))
(count-pairs (cdr x))
1)))
Show that this procedure is not correct. In particular, draw box-and-pointer diagrams representing list structures made up of exactly three pairs for which Ben’s procedure would return 3; return 4; return 7; never return at all.
Answer
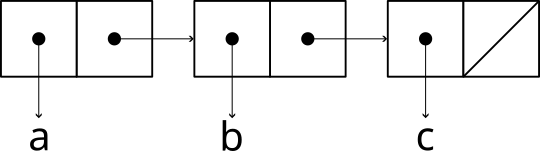
First, let’s test the simplest case in which the procedure actually returns the
correct result (3):
(list 'a 'b 'c)
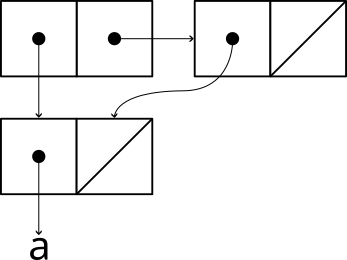
Then let’s try getting some incorrect results. This next one returns 4.
(define x (list 'a))
(list x x)
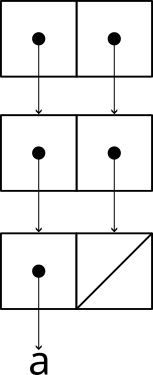
This next one returns 7:
(define x (list 'a))
(define y (cons x x))
(cons y y)
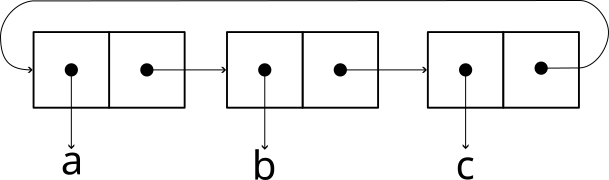
And then we can use our old make-cycle function to create an endless loop,
which will never return.
(define x (list 'a 'b 'c))
(set-cdr! (last-pair x) x)