SICP Exercise 2.71

Question

Suppose we have a Huffman tree for an alphabet of \(n\) symbols, and that the relative frequencies of the symbols are \(1,2,4,\dots,2^{n−1}\). Sketch the tree for \(n=5\); for \(n=10\). In such a tree (for general \(n\)) how many bits are required to encode the most frequent symbol? The least frequent symbol?

Answer

The trees are very unbalanced:

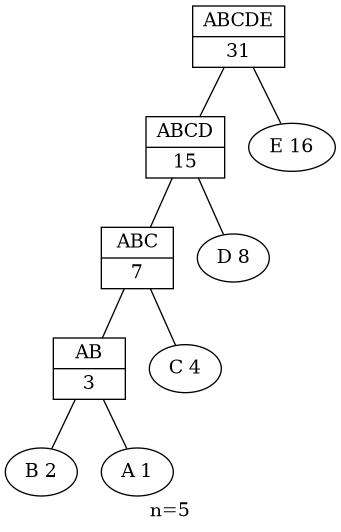
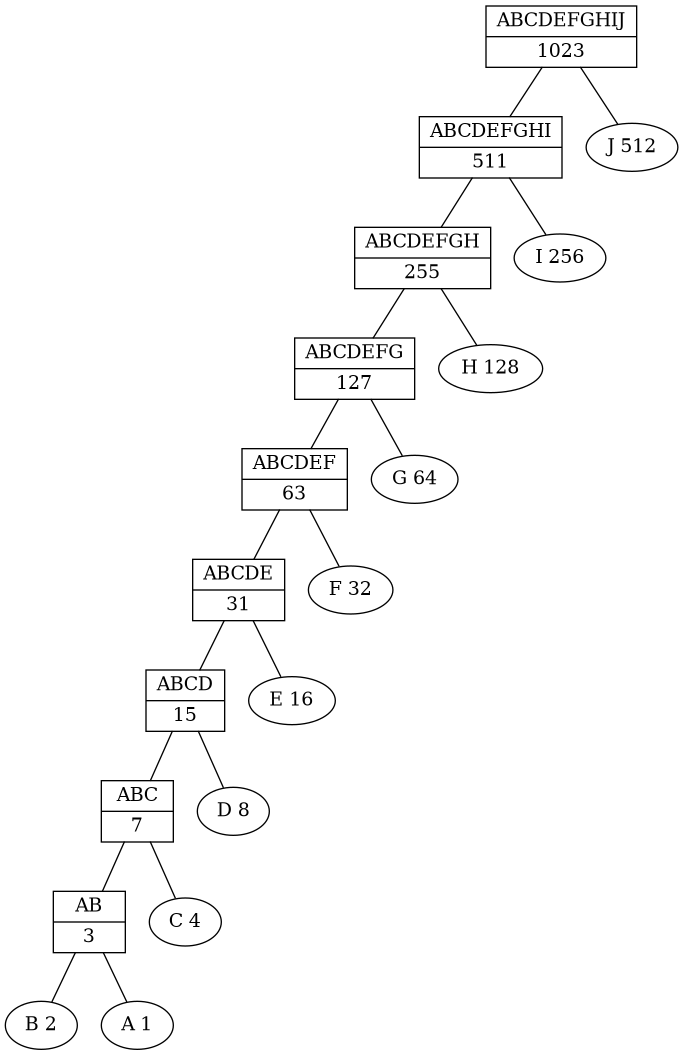
In the best-case scenario, you only need \(1\) bit to encode a symbol. For the least frequent symbol, however we need \(n-1\) bits.