SICP Exercise 2.64

Question

The following procedure list->tree converts an ordered list to a balanced binary tree. The helper procedure partial-tree takes as arguments an integer n and list of at least \(n\) elements and constructs a balanced tree containing the first \(n\) elements of the list. The result returned by partial-tree is a pair (formed with cons) whose car is the constructed tree and whose cdr is the list of elements not included in the tree.

(define (list->tree elements)
  (car (partial-tree
        elements (length elements))))

(define (partial-tree elts n)
  (if (= n 0)
      (cons '() elts)
      (let ((left-size
             (quotient (- n 1) 2)))
        (let ((left-result
               (partial-tree
                elts left-size)))
          (let ((left-tree
                 (car left-result))
                (non-left-elts
                 (cdr left-result))
                (right-size
                 (- n (+ left-size 1))))
            (let ((this-entry
                   (car non-left-elts))
                  (right-result
                   (partial-tree
                    (cdr non-left-elts)
                    right-size)))
              (let ((right-tree
                     (car right-result))
                    (remaining-elts
                     (cdr right-result)))
                (cons (make-tree this-entry
                                 left-tree
                                 right-tree)
                      remaining-elts))))))))

1. Write a short paragraph explaining as clearly as you can how partial-tree works. Draw the tree produced by list->tree for the list (1 3 5 7 9 11).
2. What is the order of growth in the number of steps required by list->tree to convert a list of \(n\) elements?

Answer

partial-tree splits up the tree (and subtrees, recursively) into three parts: the element at the top i.e. the current entry, then the left tree and the right tree. The sizes of the left and right subtree are calculated as follows:

\[ s_l = \lfloor\frac{n-1}{2}\rfloor \] \[ s_r = n-s_l \]

This allows the function to handle both odd and even numbers for n. If the number is even, the right subtree will contain one more element than the left one. Otherwise, they contain the same number of elements.

The left subtree is then built up by calling partial-tree on the original elements list with n being set to \(s_l\). Since the first elements of the list are always the smallest, this works. This is also the reason why the list needs to be ordered.

Ultimately, this will return a properly formed left subtree. Now we know that all the elements of the original list we didn’t use before now have to go into the right subtree or be set at the top of the tree as the current entry. Of course, the first number is the smallest of these, so it should not go into the right subtree, but become the current entry. All the remaining elements then form the right subtree.

This is what the tree looks like:

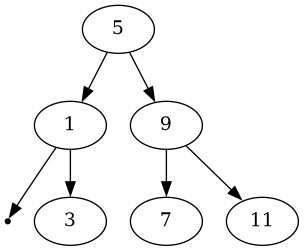
As for the complexity, I think it should be \(\Theta(n)\), since the partial-tree function is going to be called for every single list element. make-tree is also \(\Theta(n)\) and cons is just \(\Theta(1)\), so I think it makes sense.