SICP Exercise 1.24

2021-09-04

Question

Modify the timed-prime-test procedure of exercise 1.22 to use fast-prime? (the Fermat method), and test each of the 12 primes you found in that exercise. Since the Fermat test has \(\Theta(\log{n})\) growth, how would you expect the time to test primes near 1,000,000 to compare with the time needed to test primes near 1000? Do your data bear this out? Can you explain any discrepancy you find?

Answer

(define (square x) (* x x))

(define (expmod base exp m)
  (cond ((= exp 0) 1)
        ((even? exp)
         (remainder
          (square (expmod base (/ exp 2) m))
          m))
        (else
         (remainder
          (* base (expmod base (- exp 1) m))
          m))))

(define (fermat-test n)
  (define (try-it a)
    (= (expmod a n n) a))
  (try-it (+ 1 (random (- n 1)))))

(define (fast-prime? n times)
  (cond ((= times 0) true)
        ((fermat-test n)
         (fast-prime? n (- times 1)))
        (else false)))

(define (timed-prime-test n)
  (start-prime-test n (runtime)))

(define (start-prime-test n start-time)
  (if (fast-prime? n 5)
      (report-prime n (- (runtime)
                         start-time))))

(define (report-prime number elapsed-time)
  (display number)
  (display " *** ")
  (display elapsed-time)
  (newline))

; ----solution----
(define (search-for-primes lower upper)
  (cond ((even? lower) (search-for-primes (+ lower 1) upper))
        ((> lower upper) (newline))
        (else (timed-prime-test lower)
              (search-for-primes (+ lower 2) upper))))

; ----run----
(search-for-primes 1000000 1000038)
(search-for-primes 1000000 1000038)
(search-for-primes 1000000 1000038)

(search-for-primes 10000000 10000105)
(search-for-primes 10000000 10000105)
(search-for-primes 10000000 10000105)

(search-for-primes 100000000 100000040)
(search-for-primes 100000000 100000040)
(search-for-primes 100000000 100000040)

(search-for-primes 1000000000 1000000030)
(search-for-primes 1000000000 1000000030)
(search-for-primes 1000000000 1000000030)

Results:

1000003 *** 5
1000033 *** 5
1000037 *** 4

1000003 *** 4
1000033 *** 5
1000037 *** 5

1000003 *** 5
1000033 *** 5
1000037 *** 5

10000019 *** 5
10000079 *** 6
10000103 *** 6

10000019 *** 5
10000079 *** 5
10000103 *** 6

10000019 *** 5
10000079 *** 5
10000103 *** 5

100000007 *** 6
100000037 *** 7
100000039 *** 7

100000007 *** 7
100000037 *** 6
100000039 *** 6

100000007 *** 5
100000037 *** 6
100000039 *** 6

1000000007 *** 6
1000000009 *** 7
1000000021 *** 7

1000000007 *** 7
1000000009 *** 7
1000000021 *** 7

1000000007 *** 7
1000000009 *** 6
1000000021 *** 6

And another iteration, this time running the Fermat test 100 times rather than 5 times:

1000003 *** 88
1000033 *** 85
1000037 *** 88

1000003 *** 87
1000033 *** 86
1000037 *** 87

1000003 *** 87
1000033 *** 85
1000037 *** 87

10000019 *** 103
10000079 *** 106
10000103 *** 105

10000019 *** 102
10000079 *** 106
10000103 *** 105

10000019 *** 103
10000079 *** 113
10000103 *** 106

100000007 *** 119
100000037 *** 122
100000039 *** 127

100000007 *** 118
100000037 *** 122
100000039 *** 121

100000007 *** 118
100000037 *** 121
100000039 *** 121

1000000007 *** 130
1000000009 *** 129
1000000021 *** 132

1000000007 *** 130
1000000009 *** 129
1000000021 *** 135

1000000007 *** 131
1000000009 *** 129
1000000021 *** 131

Both of these are a lot faster than what we saw in the previous iterations of this exercise. This makes sense, because \(\Theta(\log{n})\) is a much slower growth rate than the \(\Theta(\sqrt{n})\) from the previous versions. For comparison, here is a graph showing \(f(x)=\sqrt{x}\) in red and \(f(x)=\log{x}\) in blue:

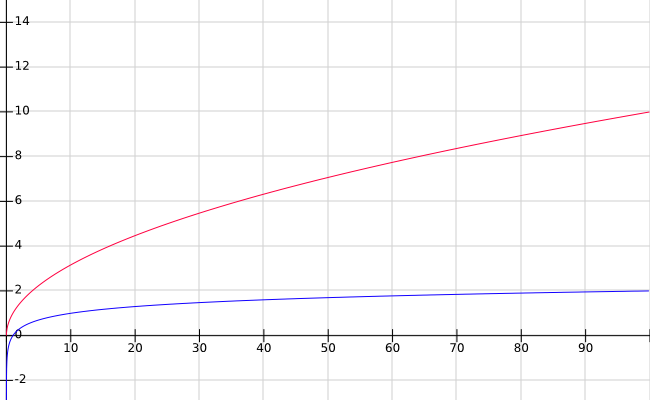
The difference between these two lines becomes massively greater as \(x\) grows. At the scales we are dealing with in this exercise, they can be huge. For comparison: \[ \sqrt{1000000000}\approx 31622.78 \] \[ \log{1000000000}\approx 20.72 \]

Of course, the number of steps depends on the amount of times we run the Fermat test. If, as in this example, we run it 100 times rather than 5 times, obviously we will have 20 times more steps for each single calculation, which is reflected in the runtime.

Let us compare our new results to those from the previous exercise and see if it confirms our expectations. We also analyse the relationship between the result of the 5-fold Fermat test to the logarithm of \(n\) vs. the 100-fold Fermat test to see if there is a relatively constant result.

Lower Bound	1.22 Time	Fer(5)	Fer(100)	Ratio Fer(5)/log	Ratio Fer(100)/log
1,000,000	15.22	4.78	86.67	0.346	6.271
10,000,000	47.89	5.33	105.44	0.331	6.541
100,000,000	151.22	6.22	121.00	0.338	6.569
1,000,000,000	469.78	6.67	130.67	0.322	6.306

As we can see, there appears to be a constant relationship between \(log(n)\) and \(Fermat(n)\). For the 5-fold Fermat test, this ratio hovers between approximately \(3.2\) and \(3.5\). In the case of the 100-fold Fermat test, the ratio also seems to be relatively constant between \(6.2\) and \(6.6\).