SICP Exercise 1.14

Question

Draw the tree illustrating the process generated by the count-change procedure of section 1.2.2 in making change for 11 cents. What are the orders of growth of the space and number of steps used by this process as the amount to be change increases?

Answer

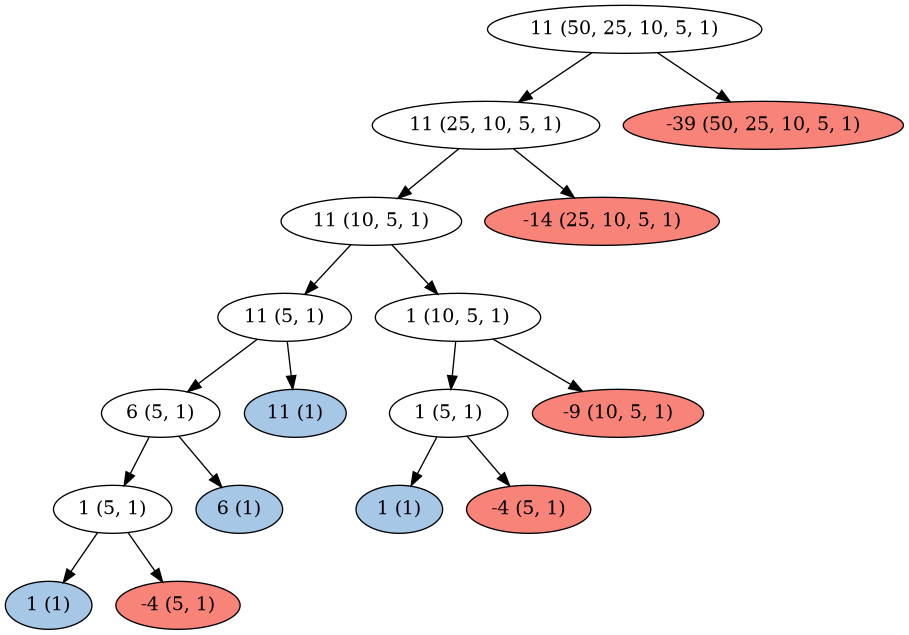
Here is the order of growth for for count-change with the amount a as the first value and the types of coin within parentheses. Leaves coloured in red return 0 and leaves coloured in blue return 1. I have also shortened the diagram somewhat since otherwise it would have become too large to fit on the screen. Specifically, any time only one type of coin is left over, it is instantly counted as evaluating to 1. This makes sense, as you only have one way to make change if all you have is 1-cent coins.

Let us analyze the space requirements first, as this should be somewhat easier.

What do we need to keep track of at every point in the process? Only the parent nodes of the current node. Therefore, the space requirements here grow linearly, giving us $\Theta(n)$. This is the same as with the Fibonacci tree we saw earlier.

How about the number of steps?

For this, let us first consider a situation in with we have only one type of coin available to us. What would the graph look like in such a scenario?

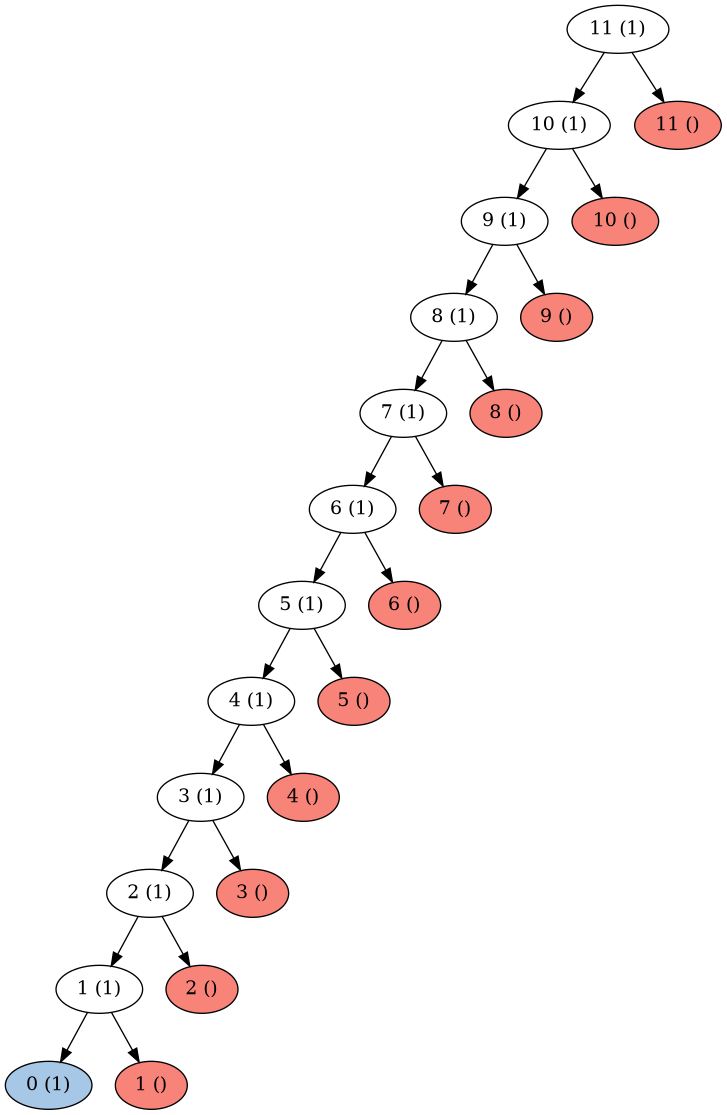
The total number of nodes here is 25 or $2a+1$. Since this is a linear relationship, we have $\Theta(n)$. So let us keep that in mind. Next, let us review a scenario in which 2 coins are available to us.

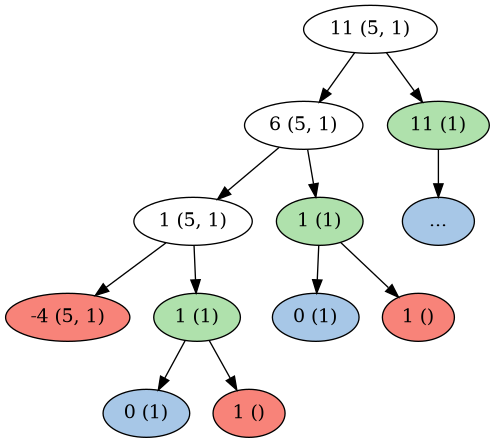
This tree now has 36 nodes. As we can see, the part on the right is exactly the same as in the previous tree in which we had only one coin, which, as we remember, had $\Theta(n)$.

If we follow the tree down the leftmost side, we see that each node contains the count-change process, with a being decremented by 5 (the value of the largest coin) on each iteration. Each single one of these iterations spawns a new subtree with one coin, highlighted in green.

The total number of spawned subtrees can be expressed as $\lceil\frac{a}{5}\rceil$ ($\lceil\frac{11}{5}\rceil=3$). This gives us a growth rate proportional to $a$ for the amount of new subtrees, each of which has a growth rate proportional to $a$ itself. Since this contains a multiplication of $a$ with itself, the growth rate is exponential: $\Theta({n^2})$.

We can already guess what happens in the case of three coins. Let us take a look at the graph:

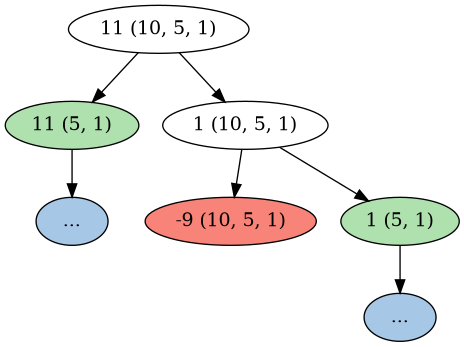
As expected, this creates $\lceil\frac{a}{10}\rceil$ new subtrees (highlighted in green), which we know have a growth rate of $\Theta({n^2})$, making the growth rate in this case $\Theta({n^3})$.

I will spare you the implementations of the same process for four and five coins, but the result is the same.

The growth rate for the number of steps with 5 coins would therefore be $\Theta(n^5)$.